Counting Topologically Distinct Directed Acyclic Graphs with Marshmallows

I wrote a miniature Ruby gem to topologically sort a Directed Acyclic Graph (DAG), which is useful when you have a bunch of things that depend on each other (e.g. tasks), and you want to put them in a linear order.

Writing the test suite got me thinking about how to find all the topologically distinct directed acyclic graphs with number of vertices V and edges E. My current algorithm goes like this:

1. Start with some large number n of toothpicks and marshmallows.

2. Call the children.

3. Try to finish before all the marshmallows are gone.

Here is what we ended up with for all graphs of V = 4:

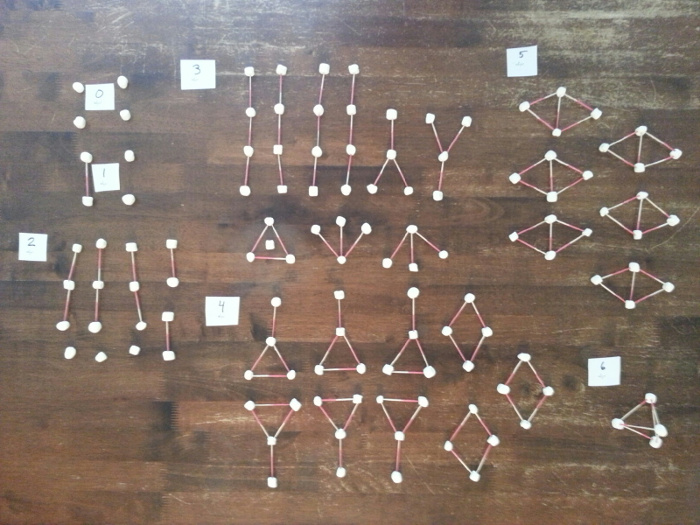
It’s not bad I think, but is a method known that works even without children? Are there any graphs I missed?

(Full disclosure: I redid this photo a couple days later with better-colored toothpicks, so now you can tell which way they point. Marshmallows may be crunchier than they appear.)

blog comments powered by Disqus Prev: An nginx HTTP-to-HTTPS Redirect Mystery, and Configuration Advice Next: Temporal Databases Annotated Bibliography